Exemplo de aproximação de um histograma por uma função de Gauss

Exemplo de aproximação de um histograma por uma função de distribuição gaussiana

Objetivo:	Mostrar através de um exemplo simples o procedimento para o cálculo da função de densidade de probabilidade Normal (Função de Gauss) através do histograma de um ruído branco.

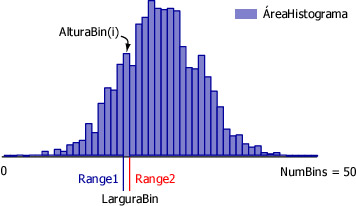
O que é um histograma?	Histograma é um gráfico, usualmente representado em forma de barras, que apresenta agrupamentos de um conjunto de dados em células ou bins. A faixa dinâmica (range) dos dados é dividida em um determinado número de bins de mesmo "comprimento". A "altura" de cada bin é dada pela contagem do número de dados contidos na faixa.

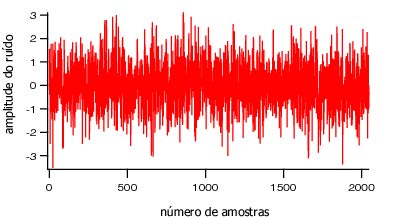
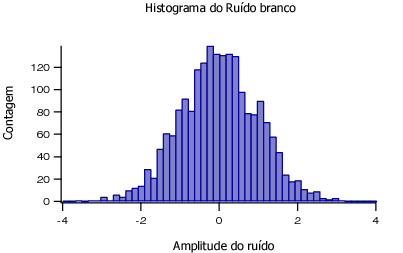
Exemplo:	Geramos 2048 amostras de um ruído branco centrado, i.e. média zero (m=0), variância igual a 1 (s²=1). A figura 1 apresenta a forma temporal deste ruído e a figura 2 mostra o histograma do ruído calculado para 50 bins.
	Figura 1 - Ruído branco N(0,1) com 2048 amostras.

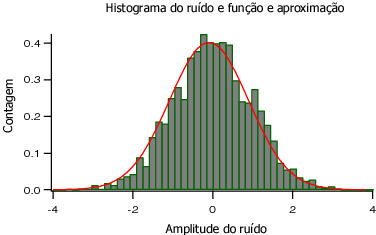
	Figura 2 - Histograma do ruído branco acima com 50 bins.

	Constatamos facilmente, a partir da figura 3, a forma da distribuição gaussiana do histograma do ruído branco. Podemos observar que o maior número de amostras encontra-se próximo a amplitude 0.
	Figura 3 - O Histograma do ruído é uma projeção deste no eixo y. Desta forma, neste exemplo, contamos o número de ocorrências do sinal em 50 faixas (bins) distribuídas igualmente sobre y.

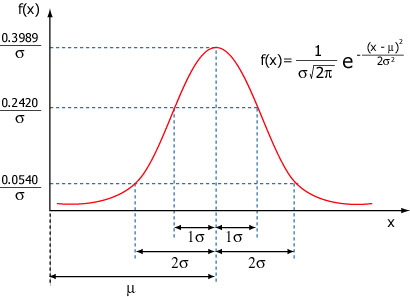
A Função de densidade de probabilidade normal	A função de densidade de probabilidade normal, bem como sua forma análitica está mostrada na figura 4. Os dois parâmetros que definem a distribuição são m, a média, e s, o desvio padrão. A integral da função, ou seja a área da curva é unitária. A área dentro de +ou- 1s centrado na média é aproximadamente 0.68. Dentro de +ou- 2s é de 0.95. Uma interpretação do significado destes valores é a probabilidade que um variável aleatória com distribuição normal, tenha seu valor maior que 2s é de aproximadadmente 0.05.
	Figura 4 - Função de densidade de probabilidade normal.

O histograma do ruído é uma função de Gauss?	Para verificarmos se a distribuição do ruído, apresentada na figura 1, é uma distribuição normal, devemos normalizar a área deste histograma. O método mais simples para calcularmos a área deste histograma é através da integração retangular, onde somamos as alturas dos retângulos multiplicando-as pela largura dos bins.
	Figura 5 - Cálculo da área do histograma do ruído branco.

	LarguraBin = Range2 - Range1 ÁreaBinNorm(i) = LarguraBin/numpontos * AlturaBin(i); ÁreaHistograma = sum(ÁreaBinNorm(i)) para i=0 até NumBins

	O passo seguinte é ajustar(fitting) o histograma e assim obter os valores de média m=0 e desvio padrão s=1, conforme apresentado na figura 6.

	Figura 6 - Histograma do ruído branco normalizado (verde) ajustado por uma função gaussiana (vermelho).

	Os valores encontrados no ajuste nos mostraram que os dados têm uma distribuição normal conforme esperado.

Ultima atualização: 21/02/2003